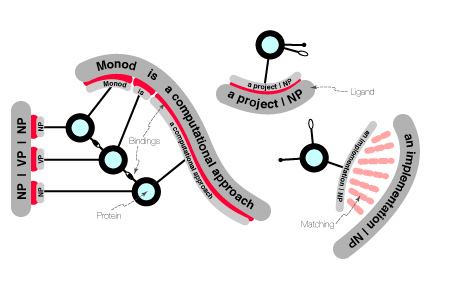
The present documentation describes in detail the computational approach of Monod. We present here an overview. This overview takes the form of a mental image.
The traditional Turing / von Neumann model posits a single program acting on data in a sequential, well-defined fashion. The action consists of different types of operations, such as arithmetic, logical operations and branch operations.
In contrast, the Monod model, called the Monod Cell, consists of a multitude of small programlets, which we call proteins by analogy with biology, all acting on the same data at the same time and interacting with one another. The data consist of strings, imagined floating along with the proteins, and are called ligands. The basis of interactions between and among proteins and ligands is matching, whereby active sites on the various entities recognize each other. Matching leads to binding and triggers actions. The actions of the proteins on ligands include the modification, breakage and linkage of segments of ligands. The actions of proteins on each other include modification of internal state. For instance, proteins may act as regulators of other proteins through expression of certain characteristics or repression of others. (As we mentioned earlier, Jacques Monod was instrumental in the discovery of regulation mechanisms between proteins. This aspect of our program is why it is named after him.) The following figure displays the elements discussed above.

The protein actions, including recognition, all take place in parallel. There is a restriction that each binding site on string or on a protein may participate in at most a single binding. While each protein's behavior is completely deterministic, the bindings are not, so that a program consisting in a set of proteins may act non-deterministically. This non-determinism may be either a feature or a bug, depending on the intention.
The proteins in the Monod model are assembled out of a finite number of building blocks according to precise instructions. The buildings blocks, called domains, can be combined in myriad ways to create proteins which perform different actions. The set of available domains is rich enough that the computing model is Turing complete. In fact, the model looks like a soup of Turing machines working on the same set of tapes. At the same time, the domains are individually powerful enough that one speaks of combinations of domains, in a way that one does not speak of the source code of a program as a combination of letters. This makes it possible to practically consider the domains as evolutionarily terminal and apply genetic algorithms to Monod programs.
The Monod Cell also includes other computational mechanisms inspired by biology. The intake and processing of data strings is the analogue of the cell feeding and transforming its intake into useful products or rejecting them. These processing steps affect an overall energy level, which is closely linked with the fitness of the cell. The cell can be subdivided into compartments, and elements (data or proteins) shuttled from one compartment to another, or from one cell to another, to increase computational performance. And so on.
FIXME: Insert graphic
Finally, Monod lends itself naturally to evolutionary algorithms. The task performed by a Monod Cell is specified by that cell's genome. The genome is then the analogue of a computer program in the Turing / von Neumann world. Perhaps because of the fact that Monod genomes are strongly inspired by the world of biology, they fit very well in the contect of evolutionary algorithms. Evolving Monod genomes is analoguous to evolving programs using, say, genetic programming. However, Monod genomes possess many desirable properties which make them possibly more suitable to these techniques.
In the rest of this section, we introduce the a hierarchical structure which helps explain the Monod approach and implementation. We also present an overview of the results obtained using Monod.