The Swarm design pattern extends the functionality of the Hive by adding formalized interactions between the residents. Each resident may have zero, one or more projections, which are fixed for the lifetime of the resident and are individually identifiable by the resident code. Each projection is tagged with a marker structure, which is initialized and changeable at the discretion of the resident. Each projection can be either active or inactive. Given two active markers, the Swarm can calculate a list of matchings between these two markers. There can be no matching (in which case we say the projections don't match), a single matching (an unambiguous match), or many matchings (ambiguous matchings — for instance, if a regular expression matches many substrings of a string). Each matching is further associated with an affinity, which is an integer representing the strength of the matching. This integer is non-zero if and only there is a match between the two markers. A particular Swarm collects all the markers from all the active projections of all the residents, and calculates and attempts to execute the matchings. Executing a matching means turning it into a binding by calling an appropriate method on each of the two residents involved. If both method calls are successful, the binding is made and both projections are removed from the list of active projections, so that they will not participate in further matchings. If either method call is unsuccessful, the binding is not made. Bindings can be released later on at the request of either resident, or of the harness. Any projection can be made active or inactive at the whim of the resident code. Making a bound projection inactive triggers an automatic release. If there is more than one matching involving the same projection with the same affinity, a single one is picked at random. The randomness introduced here injects a probabilistic flavor to this pattern, which suffuses the rest of Monod in an essential way, adding to the random click scheduling introduced in the Hive. We will return to this aspect many times throughout the documentation. FIXME: Insert graphic.
The probabilistic nature of matching operates with the following two constraints. First, if there is any matching possible, a binding operation will be triggered within a bounded time (FIXME: can we specify “one click”?). Second, the probability of a matching is proportional to the affinity between the two markers. As the affinity can not be zero if there is a matching, we are assured that all matchings have some chance to become bindings.
Collectively, the types of the projections, markers, matchings and bindings are called the exposure of the Swarm. They can be defined independently from the residents. Like the Hive, the Swarm requires a harness to control its execution. In addition to being responsible for the activation state of the Swarm and for adding and removing residents, the Swarm harness has an additional ability: it can order the release of bound residents. This behavior can be as simple as not doing anything, since residents are perfectly capable of releasing their bindings on their own. Or it can be significantly more complex, as we will see in the Cytoplasm layer (see The Cytoplasm). In real biological systems, proteins interact with each other first by recognizing each other through a matching process. This molecular recognition process is an extremely complex physical phenomenon, relying on quantum mechanical and thermodynamic effects, and has sometimes been called Brownian search to emphasize its computational role. An analogy which has been made often (since the late 19th century) is with the fit between a lock and a key. However, the Swarm presents a much more symmetrical view of the matchers than what lock and key might lead one to imagine. Projection matching in the Swarm is but a very simplified analogue of molecular recognition, and we can only hope that we've extracted some of the essence of the process rather than missed it altogether. Certainly, Monod does not benefit from the performance afforded by a real physical system due to the highly parallel nature of the microbiology — at least as long as it is implemented on traditional computing hardware. However, maybe we can still achieve some of the goals stated in the introduction. The Swarm design pattern should be used when a large number of programs should be thought of as executing concurrently, and interacting with each other. A Swarm can be the foundation for many different developments: a host of interacting and self-regulating agents, with one or more distinguished residents serving as scratch pads; Selfridge's Pandemonium; a Hive, if no resident has any projection; an artificial life competition where small programs vie with each other for dominance; or finally, for the Incubator model, discussed next. We now give more precise details of the abstract Swarm model. The interested reader should refer to the signature source file swarm.mli, which contains the abstract definitions of a Swarm, with no reference to the implementation. Like other parts of the Monod project, the Swarm is a simulation-dependent algorithm. Details of the implementation can be found in The Swarm Design Pattern Implementation.
FIXME: Precise definitions and details.
The binding operation between two residents can be decomposed into two distinct steps: docking and propagation. Both steps are independently visible to the residents. Docking is the initial step of binding. It is a sort of handshake between both residents. The result of a successful docking is that the residents have indeed agreed to bind, and a binding object has been computed. The binding object contains enough information to undo the binding. Docking may fail for any reason, at the discretion of either resident. In case of failure, the state of the system is restored to what it was before the binding initiation.
When docking is complete, propagation is initiated on each of the two residents. Propagation is guaranteed to be called atomically with docking. That is, no other operation (clicking or other binding) can have been launched involving either of the residents. During the propagation phase, the residents are free to use the information encoded by the binding. For instance, they can trigger its release, which they could not do during the docking phase since the binding was not yet consumated. However, in contrast to docking, propagation is expected to never fail.
FIXME: Insert sequence diagram
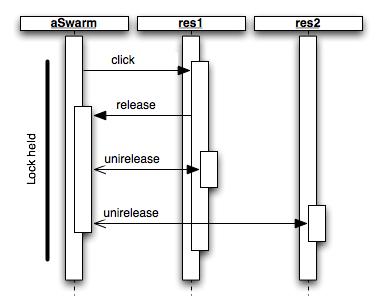
The most subtle aspect of the Swarm model concerns the release of bindings. A binding may be released in two different ways: the release can be ordered by the harness or can be ordered by one of the two residents involved in it. In the latter case, the resident may be in one of many different hooks, namely, its click method, unimate or even in unirelease, so that we have a recursive cascade of releases. The subtlety comes from the fact that when a resident orders a release, the resident is called back to change its state in order. If the resident is called while it is in the middle of its click method, for instance, then we get a complicated calling structure. The following sequence diagram is a representation of this structure.

This calling sequence structure violates our principle that resident code be logically single-threaded. The state of the resident during execution becomes difficult to understand. Hence, the Swarm model calls for a different release calling sequence, which does not thread the resident code. When a resident demands a release, from its click method or any other part of the resident code, the demand is simply queued by the Swarm and executed after the caller has returned. This new calling structure is shown in the following sequence diagram.
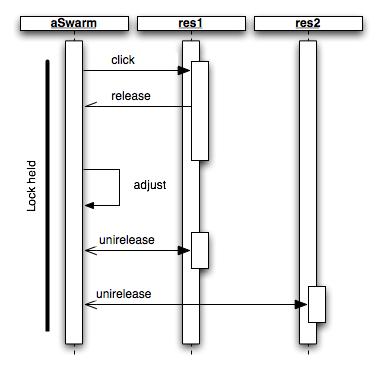
The “adjust” call represents the Swarm structure changing its internal state to reflect the release. Hence, the Swarm is updated before the resident unirelease methods are called. This calling sequence should be kept in mind when creating Swarm residents.