The Monod computational model can be described most easily if we show how it is different from the Turing / von Neumann computational model. We do this in several steps, keeping track of the relevance of each step to the end goal of the project: to provide a computational model naturally well suited to evolutionary algorithms.
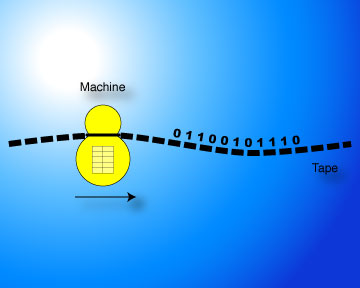
In the abstract Turing machine model of computer execution and storage, a tape is read and modified by a head according to the state and the instructions stored in an action table on the machine.
The traditional implementation of this abstract model today is the von Neumann architecture, with storage for both data and the specification of the action table (the program), and a processing unit which executes the action table.
Despite many efforts, some of them even fairly successful, the Turing / von Neumann computational model does not lend itself naturally to techniques through which the program can be evolved using well-known algorithms adapted from biology. For instance, it is difficult to define mutations and recombinations of programs. This situation has left humans as essentially the only programmers to date. However, programming is an inherently inhuman task.

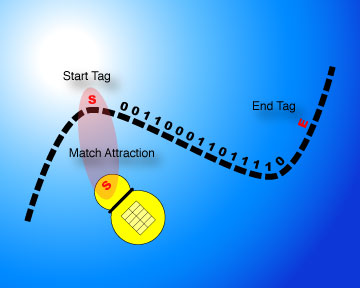
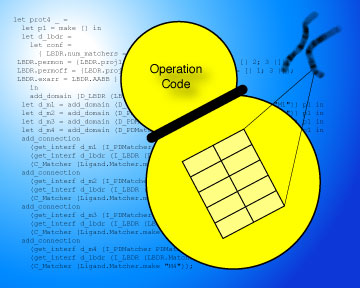
Imagining ligands and processing units may evoke the traditional picture of a Turing machine, with the ligand taking the role of the “tape” and processing units taking the role of the machine proper. One can either imagine a single processing unit sliding across the ligand in either direction (using the sliding commands described earlier FIXME: they don't exist yet), or a sequence of processing units matching and releasing the ligand and modifying it to insert a unique mark where appropriate, with the processing units always matching the mark. Hence, at the very least, the Incubator can simulate a Turing machine. Woohoo! It's easy to imagine that the machine and the tape start out in a separated state. The machine is idle in this unattached state. It possesses a matching element which may or may not correspond to a specific matching site on the tape. Through some agency, the matching element and the matching site are bound, triggering processing of the tape by the machine, as above. The machine can be separated from the tape again, according to its action table, for example when encountering an end signal on the tape.
There is no functional novelty introduced here. This step is merely necessary to pave the way for the next one. However, a crucial implementation aspects should be pointed out. Finding appropriate matchings that can trigger bindings is, properly speaking, a computational task. However, it is not a task that is performed by the machines that are posited to be part of the Monod model. It can be thought of as being performed by the ambient medium — in any case, outside of the machines. A matching element is merely an indicator. Monod-the-computational-model, where matching can be taken for granted, should thus be distinguished from Monod-the-implementation, where matching is a significant part of the program.
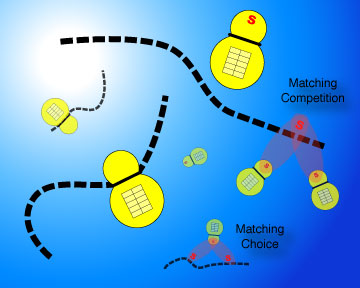
We now simply imagine that many different tapes and many different machines participate in communal execution and matching. There can be many different matching elements and matching sites. Many matching elements may compete for binding with a specific matching site on a tape, but only a single machine can be bound to a given site at any time. Conversely, many sites can compete for the attention of a single matching element on a machine. In such cases of competition, decisions are made stochastically.
The overall computation executed by the set of machines is not confined to any particular program, but is now distributed among the various programlets of each machine. Their action is coordinated through the matchings: a machine can create a matching site for another machine by changing the tape it is attached to; a machine can alter its matching element; the probabilistic nature of matching implies that the course of execution is not necessarily entirely determined by the set of individual programlets of all the machines; etc.
A most notable property of this program execution environment is that conditional branching can be (though does not need to be) eliminated from the repertory of instructions available to program each individual machine. Introduced very early on in its modern intent, the first description of conditional branching was fairly murky (Turing described it as an unconditional branch preceded by a computation which modified the code!). It is notoriously difficult to deal with branching in contemporary programming, because of the complexity it introduces, yet is indispensable — because of the complexity it introduces. Think of all the effort, both practical and theoretical, expended in white box tests, black box tests, debugging, dead branches, etc. The Monod computational model offers a very different way to think about conditional branching: indeed, a conditional branch can always be replaced by a tape/machine separation followed by the conditional binding of one of two machines depending on the state of the tape at the time of separation. FIXME: impact? On reusability, modularity, encapsulation — and more?
Another notable property of the environment is a natural suitability to parallel program execution. Many machines can be running at the same time on the same or different tapes.
The implications of this step on the evolvability of programs are
significant. Conditional branching is a notoriously difficult
instruction to deal with through evolutionary techniques — perhaps the
difficulty can be mitigated by treating this instruction differently,
as described above. The subdivions of a program into many programlets
introduces the possibility of natural homologous recombination, which
is absent from most current models of genetic programming. Programs
evolved in this computational environment have a fighting chance of
being natural candidates for parallel execution.
Parallelism is indeed apparent in the above mental image, since many “programs” can work at the same time on the same data set. However, the situation may appear rather unruly, with all sorts of thingies bumping against one another. Of course, this is what happens inside a real biological cell. But even more importantly, there's no reason that the Turing soup be fundamentally disordered. It needs to be “programmed” well, just like a regular Turing machine — that is, it needs an appropriate set of processing units — like the deterministic programs discussed in the previous section.
FIXME: Relate definitions in previous section with Halting problem for Turing machines.
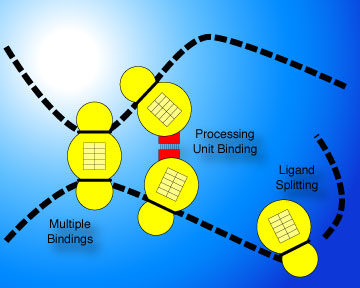
In addition to the binding and releasing of tapes and moving along them, machines can be equipped with additional powers. For instance, tapes can be split and joined. Machines can be equipped with matching elements that match with other matching elements on other machines in order to affect both matchines' internal state. A machine can have more than a single matching element. And so on.
Wisely or unwisely, in order to define the operations allowed, we derive much inspiration from the molecular biology of cells. An analogy drives this inspiration, whereby machines are identified with proteins and tapes with polynucleotides (which we call ligands in the model).
From an evolutionary perspective, the operations available are a subset of the atomic instructions available to the programs in the Monod model. Having more complex operations available does not change the functional range of the model, but possibly significantly alters the operational characteristics such as speed of execution, speed of evolution and size of the programs.
The specification of each machine includes the matching elements, the action table and how these two entities are related to one another. As with traditional Turing machines, there are different ways to define the specification of a machine in the Monod model: through an actual state table or through a program in a suitable language, for instance.
Each machine in the Monod model is assembled out of a finite set of specific domains, according to a blueprint for the machine. Each domain type has a specific function — for instance, a matching element domain, or an arithmetic operation domain — and can be connected to other domains through interfaces that it expresses — for instance, a matching element domain expresses a "I'm bound now" interface.
Constructing the machines out of domains provides yet another level of genetic flexibility to the Monod model. Each machine is described by a set of domains and a set of connections between the interfaces of these domains. This description is akin to a gene and is highly amenable to controlled mutation and recombination.
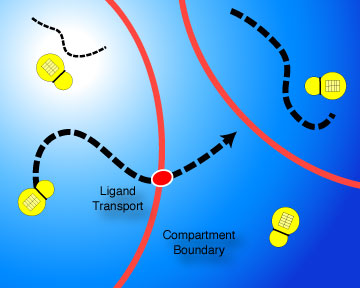
Binding and execution take place within bounded compartments. They are filled with a medium within which float the tapes and machines, which bump against one another, binding when matching is present.
Compartments may adjoin one another and tapes or machines may be transported from one to the other according to specific rules. Compartments may keep global computational variables, such as energy, which is depleted through certain operations and replenished by the presence of the end-products of successful computations.
Compartments play a powerful role in the execution model by making it possible to segregate complex computations from one another. This segregation reduces side-effects, which may be brought about through uncontrolled evolution, and it accelerates computation by increasing the probability of appropriate bindings. Both of these effects have a significant impact on the evolution of programs within the Monod model.
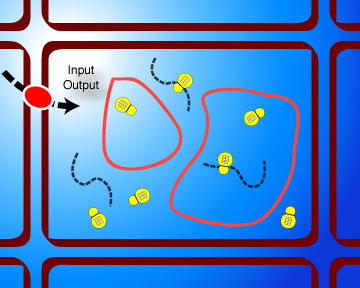
Monod cell is a complete autonomous system based on the Monod computational model. It includes one or more compartment, machine production capabilities (as in a cell nucleus) and input/output capabilities (as in a cell membrane).
A Monod cell has a genome, which contains the instructions to create the machines that run within its compartments and their expression conditions. A genome is a particular instance of a genotype, which is the class of all equivalent genomes. The genotype of a cell can be seen simply as "the program that is run by the cell". The cell itself can be seen as the corresponding phenotype to its genotype.
Does the Turing soup provide any benefit over the classical single Turing machine? It depends, first on what one cares to call a benefit and also on the particular implementation. Maybe. Ultimately, a Monod cell is really just a different way to do programming. We hope that the characteristics of the Monod cell lend the model naturally to evolutionary techniques. This alternative view of computation may have radical implications into how one perceives the task of programming. As long as the entire apparatus is implemented on a classical, Turing substrate (as it is today), it does not provide any theoretical advantage. We still can't solve the Halting problem any better, the notion of effective computability is unaffected, etc. However, the Monod computational model lends itself naturally to non-classical computational substrates. We cite three examples: widely distributed processing, which at least may provide a performance difference; truly stochastic matching and release mechanisms, possibly based on quantum effects, so that anything goes as far as effective computability is concerned; and molecular computing, which incorporates the above two examples and perhaps much more.