A.1 Two Ligand Binding Sites

This sections explores all the possible proteins which have precisely two ligand binding projection sites, no structural binding projection site and which are made out of the following domains flavors: SLBD, LBDR, LID and BMD (see Domains). We further require that all matcher inputs be static.

We can first divide this set into those proteins which perform remapping and those that don't.

A.1.1 Without Remapping

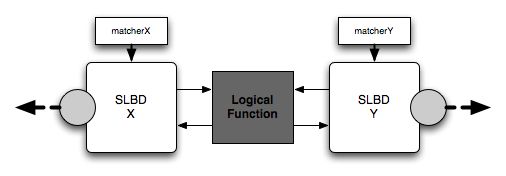
A protein with two ligand projection sites and without remapping must have exactly two SLBDs. Since we require that matching inputs be static, all we have left is to determine the mapping between the two boolean expressors and the two boolean acceptors, as shown in the following figure.

In order to complete the picture, we need to determine the logical function in the middle and to decide on whether the two matchers are the same or are different.

A.1.1.1 Truth-table Driven Logical Functions

One class of logical functions is especially simple to classify: those which settle immediately to a predictable output that depends on the input according to a simple truth table. As there are two inputs, the binding states for the SLBDs X and Y, and two outputs, the repress states for the SLBDs X and Y, there are 256 possible tables, symbolized in the figure below.

All the proteins definitions in this category are realizable as finite, stabilizing and well-defined proteins. (FIXME: Argument?)

We can arrange the 8 variables as a vector (R^X_1, R^X_2, R^X_3, R^X_4, R^Y_1, R^Y_2, R^Y_3, R^Y_4) in order to classify all the possible tables. As the system is clearly symmetrical with respect to the interchange of the X and Y SLBDs, we can omit those tables which are “under the diagonal”, which is what we do in the table below. This listing thus has 136 entries. This listing is certainly overkill, but it was useful in order to think more clearly about the issues involved. There is certainly a representation of the problem which takes into account the semantic relationships between the various entries of the truth table but sheer laziness made us go through the raw listing.

(0, 0, 0, 0, 0, 0, 0, 0)

This protein binds to two ligands and never releases them. It is thus deleterious.

(0, 0, 0, 1, 0, 0, 0, 0)

This protein can not release any ligand bound to Y. Deleterious.

(0, 0, 0, 1, 0, 0, 0, 1)

Will bind to either the X or Y ligand individually, and release both when both are simultaneously bound. This protein is potentially useful in order to conditionally control the concentration of ligands in the Cytoplasm. However, its symmetry makes it difficult to harness.

(0, 0, 1, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(0, 0, 1, 0, 0, 0, 0, 1)

Will bind to X but release it immediately. Will also bind to Y, and release it when further bound to X, at which point it will also release X. This protein can also be used to control the concentration of the Y ligand by binding to it until X is released. Hence it is useful. However, the repeated binding and releasing of X is wasteful. The same functionality is exhibited more optimally by the (1, 0, 1, 1, 0, 0, 1, 1) protein.

(0, 0, 1, 0, 0, 0, 1, 0)

This protein will never release a ligand bound to Y. Indeed, if X is also bound, then both ligands are bound and nothing will happen. Deleterious.

(0, 0, 1, 1, 0, 0, 0, 0)

Can't release Y. Deleterious.

(0, 0, 1, 1, 0, 0, 0, 1)

Same as (0, 0, 1, 0, 0, 0, 0, 1) but slightly more efficient since when bound ligands are bound, they are released together immediately. Useful.

(0, 0, 1, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(0, 0, 1, 1, 0, 0, 1, 1)

Pretty much the same as (0, 0, 1, 0, 0, 0, 0, 1).

(0, 1, 0, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(0, 1, 0, 0, 0, 0, 0, 1)

When bound to Y, will repress X. But if X is bound first, it can't be released. Deleterious.

(0, 1, 0, 0, 0, 0, 1, 0)

Can't release X. Deleterious.

(0, 1, 0, 0, 0, 0, 1, 1)

Can't release X. Deleterious.

(0, 1, 0, 0, 0, 1, 0, 0)

Can't release X. Deleterious.

(0, 1, 0, 1, 0, 0, 0, 0)

Can't release Y. Deleterious.

(0, 1, 0, 1, 0, 0, 0, 1)

This protein looks like it could be used to control the concentration of the X ligand. X will bind, until the moderator Y appears to release both. However, when Y is bound alone, X is repressed and Y will never be repressed. Hence, this protein is deleterious.

(0, 1, 0, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(0, 1, 0, 1, 0, 0, 1, 1)

Won't release if Y binds first, as X will be repressed. Deleterious.

(0, 1, 0, 1, 0, 1, 0, 0)

This protein can be used to control the concentration of the X ligand. X will bind and be released by the moderator Y. Y will then alone be bound, at which time is will be released. The functionality of this protein, however, is more optimally accomplished by another protein. Useful.

(0, 1, 0, 1, 0, 1, 0, 1)

Same as above, but slightly more efficient. Still, Y will bind and be released needlessly if it is present without X in the Cytoplasm.

(0, 1, 1, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(0, 1, 1, 0, 0, 0, 0, 1)

Y won't be released if bound first. Deleterious.

(0, 1, 1, 0, 0, 0, 1, 0)

Can't release Y. Deleterious.

(0, 1, 1, 0, 0, 0, 1, 1)

Y won't be released if bound first. Deleterious.

(0, 1, 1, 0, 0, 1, 0, 0)

Neither the X or the Y ligand will stick alone to this protein. While it won't hog any ligand, it won't do anything useful either. Useless and wasteful.

(0, 1, 1, 0, 0, 1, 0, 1)

Won't bind to anything. Useless and wasteful.

(0, 1, 1, 0, 0, 1, 1, 0)

Won't bind to anything. Useless and wasteful.

(0, 1, 1, 1, 0, 0, 0, 0)

Can't release Y. Deleterious.

(0, 1, 1, 1, 0, 0, 0, 1)

Control the concentration of Y ligand. However, X will bind and be released continuously, impairing efficiency. Useful.

(0, 1, 1, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(0, 1, 1, 1, 0, 0, 1, 1)

Control the concentration of Y ligand. However, X will bind and be released continuously, impairing efficiency. Useful.

(0, 1, 1, 1, 0, 1, 0, 0)

Won't bind to anything. Useless and wasteful.

(0, 1, 1, 1, 0, 1, 0, 1)

Won't bind to anything. Useless and wasteful.

(0, 1, 1, 1, 0, 1, 1, 0)

Won't bind to anything. Useless and wasteful.

(0, 1, 1, 1, 0, 1, 1, 1)

Won't bind to anything. Useless and wasteful.

(1, 0, 0, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 0, 0, 0, 0, 0, 0, 1)

Can't release X. Deleterious.

(1, 0, 0, 0, 0, 0, 1, 0)

Can't release X. Deleterious.

(1, 0, 0, 0, 0, 0, 1, 1)

Can't release X. Deleterious.

(1, 0, 0, 0, 0, 1, 0, 0)

Can't release X. Deleterious.

(1, 0, 0, 0, 0, 1, 0, 1)

Can't release X. Deleterious.

(1, 0, 0, 0, 0, 1, 1, 0)

Can't release X. Deleterious.

(1, 0, 0, 0, 0, 1, 1, 1)

Can't release X. Deleterious.

(1, 0, 0, 0, 1, 0, 0, 0)

Can't release X. Deleterious.

(1, 0, 0, 1, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 0, 0, 1, 0, 0, 0, 1)

Control the concentration of Y. X will behave well when Y is not present. One of the optimal representations of the functionality. Useful.

(1, 0, 0, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(1, 0, 0, 1, 0, 0, 1, 1)

Control the concentration of Y. X will behave well when Y is not present. One of the optimal representations of the functionality. Useful.

(1, 0, 0, 1, 0, 1, 0, 0)

Won't hold on to Y. Useless and wasteful.

(1, 0, 0, 1, 0, 1, 0, 1)

Won't hold on to Y. Useless and wasteful.

(1, 0, 0, 1, 0, 1, 1, 0)

Won't hold on to Y. Useless and wasteful.

(1, 0, 0, 1, 0, 1, 1, 1)

Won't hold on to Y. Useless and wasteful.

(1, 0, 0, 1, 1, 0, 0, 0)

Can't release Y. Deleterious.

(1, 0, 0, 1, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 0, 1, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 0, 1, 0, 0, 0, 0, 1)

Control the concentration of Y. X will behave well when Y is not present. However, it will be released in two steps after it binds to catalyze the release of Y. Useful.

(1, 0, 1, 0, 0, 0, 1, 0)

Can't release Y. Deleterious.

(1, 0, 1, 0, 0, 0, 1, 1)

Control the concentration of Y. X will behave well when Y is not present. However, it will be released in two steps after it binds to catalyze the release of Y. Useful.

(1, 0, 1, 0, 0, 1, 0, 0)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 0, 0, 1, 0, 1)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 0, 0, 1, 1, 0)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 0, 0, 1, 1, 1)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 0, 1, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 0, 1, 0, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 0, 1, 0, 1, 0, 1, 0)

Both ligands repressed from the start. Useless.

(1, 0, 1, 1, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 0, 1, 1, 0, 0, 0, 1)

Control the concentration of Y. X will behave well when Y is not present. One of the optimal representations of the functionality. Useful.

(1, 0, 1, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(1, 0, 1, 1, 0, 0, 1, 1)

Control the concentration of Y. X will behave well when Y is not present. One of the optimal representations of the functionality. Useful.

(1, 0, 1, 1, 0, 1, 0, 0)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 1, 0, 1, 0, 1)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 1, 0, 1, 1, 0)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 1, 0, 1, 1, 1)

Won't bind to anything. Useless and wasteful.

(1, 0, 1, 1, 1, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 0, 1, 1, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 0, 1, 1, 1, 0, 1, 0)

Both ligands repressed from the start. Useless.

(1, 0, 1, 1, 1, 0, 1, 1)

Both ligands repressed from the start. Useless.

(1, 1, 0, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 1, 0, 0, 0, 0, 0, 1)

Can't release X. Deleterious.

(1, 1, 0, 0, 0, 0, 1, 0)

Can't release X. Deleterious.

(1, 1, 0, 0, 0, 0, 1, 1)

Can't release X. Deleterious.

(1, 1, 0, 0, 0, 1, 0, 0)

Can't release X. Deleterious.

(1, 1, 0, 0, 0, 1, 0, 1)

Can't release X. Deleterious.

(1, 1, 0, 0, 0, 1, 1, 0)

Can't release X. Deleterious.

(1, 1, 0, 0, 0, 1, 1, 1)

Can't release X. Deleterious.

(1, 1, 0, 0, 1, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 0, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 0, 0, 1, 0, 1, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 0, 1, 0, 1, 1)

Both ligands repressed from the start. Useless.

(1, 1, 0, 0, 1, 1, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 0, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 0, 0, 0, 1)

When Y is bound, X can't bind to release it because it is repressed. Deleterious.

(1, 1, 0, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(1, 1, 0, 1, 0, 0, 1, 1)

When Y is bound, X can't bind to release it because it is repressed. Deleterious.

(1, 1, 0, 1, 0, 1, 0, 0)

Won't hold on to Y. Useless and wasteful.

(1, 1, 0, 1, 0, 1, 0, 1)

Won't hold on to Y. Useless and wasteful.

(1, 1, 0, 1, 0, 1, 1, 0)

Won't hold on to Y. Useless and wasteful.

(1, 1, 0, 1, 0, 1, 1, 1)

Won't hold on to Y. Useless and wasteful.

(1, 1, 0, 1, 1, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 1, 0, 1, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 1, 0, 1, 1)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 1, 1, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 0, 1, 1, 1, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 1, 1, 0, 0, 0, 0, 1)

When Y is bound, X is repressed. Deleterious.

(1, 1, 1, 0, 0, 0, 1, 0)

Can't release Y. Deleterious.

(1, 1, 1, 0, 0, 0, 1, 1)

When Y is bound, X is repressed. Deleterious.

(1, 1, 1, 0, 0, 1, 0, 0)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 0, 0, 1, 0, 1)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 0, 0, 1, 1, 0)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 0, 0, 1, 1, 1)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 0, 1, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 1, 0, 1, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 1, 0, 1, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 1, 1, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 1, 1, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 0, 1, 1, 1, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 0, 0, 0, 0)

Can't release Y. Deleterious.

(1, 1, 1, 1, 0, 0, 0, 1)

When Y is bound, X is repressed. Deleterious.

(1, 1, 1, 1, 0, 0, 1, 0)

Can't release Y. Deleterious.

(1, 1, 1, 1, 0, 0, 1, 1)

When Y is bound, X is repressed. Deleterious.

(1, 1, 1, 1, 0, 1, 0, 0)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 1, 0, 1, 0, 1)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 1, 0, 1, 1, 0)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 1, 0, 1, 1, 1)

Won't bind to anything. Useless and wasteful.

(1, 1, 1, 1, 1, 0, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 0, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 0, 1, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 0, 1, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 1, 0, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 1, 0, 1)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 1, 1, 0)

Both ligands repressed from the start. Useless.

(1, 1, 1, 1, 1, 1, 1, 1)

Both ligands repressed from the start. Useless.

• Deleterious behavior. This characterizes proteins which bind to one or more ligand and can never release it. This behavior is considered deleterious because it corresponds to a dead end for entities in the Cytoplasm. 56 of the 136 entries above, or about 41%, exhibit deleterious behavior.
• Useless and wasteful behavior characterizes those proteins which ultimately do nothing, but which spend cycles binding and later releasing ligands. The waste has a definite negative impact on the performance of the system and as such should be considered deleterious as well, but we isolated it for reasons of precision. 32 entries above, or about 24%, exhibit useless and wasteful behavior.
• Those proteins which do not bind to anything and do nothing are useless. They do consume space in the Cytoplasm but little energy is expended keeping track of them so that they are less dangerous than the wasteful proteins above. 39 entries above, or about 29%, exhibit useless behavior.
• Some proteins are useful but non-optimal. These are proteins which have a putative function but which are nevertheless wasteful of the resources of the Cytoplasm. The possible functions that have been encountered are:
  • Control of the concentration of the X ligand. This function is represented by 2 non-optimal proteins.
  • Control of the concentration of the Y ligand. This function is represented by 5 non-optimal proteins.
  We do not count as non-optimal the staggered release shown by certain proteins, which does not cost much. Hence, about 5% of the proteins show useful but non-optimal behavior.
• Finally, a few proteins exhibit useful, optimal behavior. One of them performs symmetric moderation of the concentrations of the X or Y ligands, while 6 of them perform moderation of the Y ligand exclusively, but very well. About 4% of the proteins show useful and optimal behavior.

FIXME: Discussion about how the percentages above can not be interpreted as *probabilities* that a randomly generated protein is useful or whatever, for two reasons: the listing above does not reflect the choice of genetic encoding, which is how proteins are created to begin with; and we have only listed those proteins which are simply truth-table driven. The next section shows a lot more proteins composed of the same domains, which have different short-term behavior.

A.1.1.2 Other Logical Functions

FIXME: Show examples of finite proteins which *almost* follow a truth table pattern but which arrive to it after a few oscillations. Also show non-finite proteins.

A.1.2 With Remapping

A.1.2.1 Truth-table Driven Logical Functions