In this section, we describe how to assemble multiple domains to create useful entities. The end product are proteins. They will be placed in the Cytoplasm layer of the design stack and will act as the processing units of the underlying Incubator.
The first step is the definition of an abstract domain assembly, or domain assembly for short. A domain assembly A is a pair (D = domains(A), C = conn(A)) consisting of a set D of abstract domains and of a set C of connections between domains in D. Precisely, a connection c in C is a pair (s, d) where s is an expressor interface of some domain src(c) in C and d is an acceptor interface of some domain dest(c) in C (possibly the same domain), which are such that both interfaces have the same type. We further require that any interface can not appear in two different connections. Not all interfaces need to be source or destination interfaces. Those that are not are said to be naked.
A concrete domain assembly is a domain assembly where the domains are conrete domains rather than abstract domains. If bf A is a concrete domain assembly and A is the underlying abstract domain assembly, we say that bf A is a concretization of A.
We define proj(A) to be the set of projections of all boundary domains of domains(A). If p in proj(A), then domain(p) is the domain which contains p. We trivially extend the notion of operation from domains to domain assemblies by definition an operation of a domain assembly (either input or output) a pair consisting of a projection site p in proj(A) and an operation (either input or output) of p. FIXME: Insert graphic example of domain assembly. List projection sites, identify naked interfaces, etc.
We now present a number of definitions concerning the behavior of domain assemblies. We start from a purely behavioral point of view, presenting these definitions in terms of the projection site operations that domain assemblies accept and emit.
An input history for A is a set of pairs (t, S_t) consisting of a time t and a set of input transitions S_t for A. Similarly for output history. Note that these notions clearly depend only of domains(A) — in fact, only on proj(A) — as does the following. A behavior function for A is simply a mapping from input histories to output histories. A behavior function describes how a domain assembly reacts to inputs. However the definition we have given is much too permissive. For example, it allows a domain assembly to never react or to react to nothing at all! In particular, as we have noted, the notion of behavior function is currently entirely independent from the connections of A. We make a few additional definitions in order to restrict behavior functions to make them slightly better behaved and give a few examples.
A behavior function F is finite if it maps finite input transitions to finite output transitions. Finiteness is a useful condition for proofs. A finite behavior function F is causal if input transitions can only have an impact on future output transitions. More precisely, F is causal if, for any state input histories I_1 and I_2 which are equal up to a certain time t_e, the corresponding output histories O_1 and O_2 are also equal up to t_e. Causality is a desirable property. Well, put another way, the lack of causality makes everything rather unpredictable. We can shift an operation history h by a time parameter tau to create another operation history h_tau by adding tau to the time member of each element of h. We can do this for any subset of an operation history as well. The extent of a finite operation history is the time interval from the lowest time appearing in the definition of the history to the highest. We can also make this definition for any subset of an operation history. A cut in an operation history is a time value theta which is not equal to the time of any operation in the history. Given an operation history h, a cut theta and a shift value tau, we can shift the parts of h which are later than theta by tau to create a new operation history h[theta, tau]. This operation is called spacing an operation history. A causal behavior function F is said to be spacing independent if any input history, suitably spaced, is then essentially invariant for F under the action of further spacing. More precisely, F is spacing independent if, for any input history h and for any cut theta of h, there exists a shifting value tau_0(theta) such that, for any shifting value tau > tau_0(theta),
F(h[theta, tau]) = F(h)[theta, tau].
This definition is easily extended to a finite arbitrary number of cuts. The gist of the definition is that a spacing independent function has a well-defined, canonical response to any input history. Because of causality and finiteness, we know that if we wait long enough after the last operation of an input history, we'll eventually see the entire response. Spacing independence adds the desirable property that the response does not depend on the timing of the last input operation, if it occurred late enough to begin with. Note that in particular, if we choose the cut to be before any input transition, we can shift a spacing independent behavior function by any value and obtain the same response. This comforting property is called predictability. Finally, spacing independence has an impact when passing to a discrete time value, as we will see further.
Given a spacing independent behavior function F we can create the associated behavior essence function overline F. This function accepts a finite ordered sequence of input transitions and returns a finite ordered sequence of sets of output transitions. The output is equal to the result of applying F to the input history corresponding to the input sequence, suitably spaced out so that the result will be independent of further spacing according to the definition above. It is easy to see that overline F applied to an initial sequence is equal to the initial sequence of the result of applying overline F. The behavior essence function characterizes what the behavior function does most of the time. What it does not include is what happens when input transitions are presented too fast that they can step on each other's functions. As an example, imagine that a binding operation is presented to a projection site of a domain assembly and that a release operation follows quickly, before the binding operation has had the time to “complete”. The resulting behavior might be very complex, and it is even difficult to say even what it should be. It is certainly captured by the behavior function F, but not by the behavior essence function overline F.
Two behavior functions F and F' which have the same behavior essence function overline F are said to be essentially equivalent. Hence, essentially equivalent functions differ only in they respond to closely presented input transitions. Of course, if they differ at some time t_0 then they may differ at any subsequent time even if further transitions are presented leisurely.
FIXME: Examples?
FIXME: There is some minor confusion sometimes about concretizations versus realization functions. Clean up.
All of the definitions above concerning behavior functions are very much removed from the domain assemblies they concern since, as we mentioned, they depend only on the projection sites of the assemblies and not on the connections. In order to tie behavior functions deeper with the assemblies, we need to introduce some more machinery. This machinery is related to the connections of the domain assembly.
A state of a domain assembly is an assignment c mapsto v of a value v for each connection c in conn(A) which is such that v belongs to the value set of the well-defined interface type of c. A state history for A is a time dependent assignment of a state, t mapsto c(t). The restriction of an operation history h to a domain d in domains(A) is equal to those elements of the history whose operations belong to one of the projections sites of d. Similarly, the restriction of a state history of A to a domain d of A is the function which assigns values to each acceptor and expressor interface of d such that the value assigned at time t to an interface which is either the source or the destination of a connection in conn(A) is equal to the value of that connection at the same time.
A proto realization function of a concrete domain assembly bf A is a pair (F, S) where F is a behavior function for A and S is a mapping from input histories to state histories of A. A realization function for bf A is a proto realization function which is such that its restriction to each concrete domain d in domains(A) is compatible with the conformation engine of d. FIXME: more details — we need to have defined the conformation engine more appropriately earlier.
FIXME: Any concrete domain assembly can be given a realization function: realization functions exist. In how many ways? What are the parameters?
The realization function is the glue that ties together all the components of the domain assembly. The behavior function associated with a realization function is definitely not arbitrary and must bear some relationship to the projection sites of the assembly, the domain types which exist in it and the connections between the domains. A behavior function of a domain assembly A which is associated with the realization function of a concretization bf A of A is said to be a true behavior function of A. Let's look at some properties and examples.
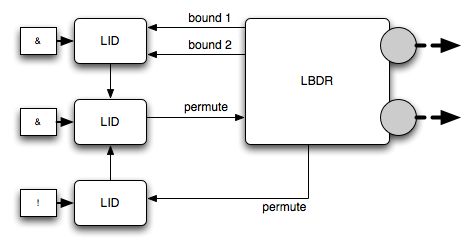
Note that a true behavior function is not necessarily finite. A non-finite behavior function will occur if we can find a cycle in the union of the state machines which does not need any external input operations to work. The following figure shows a domain assembly with a single LBDR domain which has such a cycle. (Note that only the relevant interfaces are shown.)

Whatever the realization function used to concretize the above assembly, the behavior function will go back and forth between the two permutation states as soon as both ligands are bound. Each permutation emits an output transition. Hence, the output history corresponding to the input history with two binding operations is infinite.
However, as soon as it is finite, a true behavior function is necessarily causal. Indeed, output transitions are always emitted by domains in response to input transitions and acceptor interface value changes.
FIXME: Does finiteness depend on the realization function? In the above example, it does not, but that does not need to always be the case.
Spacing independence is a bit more complex, as a true finite behavior function can be spacing dependent. As for lack of finiteness, spacing dependence is again caused by cycles in the global state machine, but this time the cycles are not manifested to the outside world: they are purely internal cycles. Consider the assembly shown in the following figure.
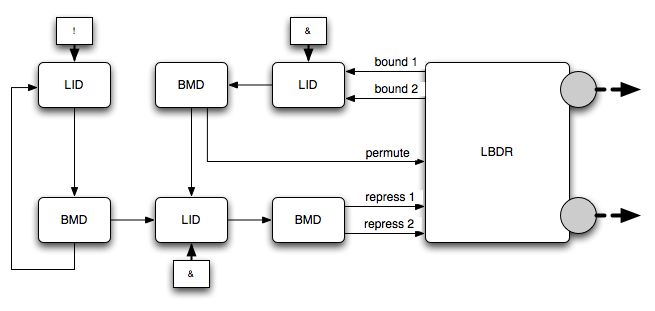
There are fundamentally different behavior functions associated with concretizations of this domain assembly representation. However, at least some of them have a conspicuously bad property: when both ligands are bound, whether they are immediately released or first undergo a remapping is unpredictable. Indeed, the two domains on the right-hand side of the figure, the negation logical integration domain and the boolean multiplexor, combine to produce an ever-oscillating true/false value which is fed to the rest of the system. If the values output from the top boolean multiplexor domain are slow enough, release will take place before the permutation occurs. Note that when both ligands are not bound, repression orders do not reach the LBDR so that the output history is indeed finite.
The choice of behavior is thus between a domain assembly which does nothing (it binds and releases) and one that does a ligand remapping. It may seem this choice is somewhat illusory, as we can simply ignore the domain assembly when it does nothing. However, the example illustrates an important property of domain assemblies and as we add more complex domains to the mix, a domain assembly can act in a much more confused fashion.
In order to address this eventuality, we introduce a property of realization functions. A state history is said to stabilize if all the values on all the connections are constant after a certain time. A realization function is stabilizing if the state history corresponding to any input history stabilizes. All domains individually stabilize. Hence, the only reason that a domain assembly would fail to be stabilizing is if there's a cycle in the assembly which creates an oscillatory behavior, as in the above example. It is easy to see that a stabilizing realization function necessarily has a spacing independent behavior function. Indeed, choose the shifting parameter tau_0 to be equal to the time it takes for the state history to stabilize. FIXME: Is the converse true? It may be, but that's not totally obvious.
Some of the definitions above have been made in terms of concretizations of domain assemblies. This situation is unsatisfying as we would like to be able to look at a graphical representation of a domain assembly and deduce its properties without having to consider particular realization functions. Hence, we make the following definitions. An abstract domain assembly A is finite if all its concretizations are finite. (FIXME: as noted above, is it sufficient to look at a single concretization?) It is stabilizing if all its concretizations are stabilizing and similarly for spacing independence.
One last property remains. The reader will have noticed that the behavior of a domain assembly can depend strongly on its concretization. Hence, a well-defined domain assembly is a finite spacing-independent abstract domain assembly such that any concretization of it has the same behavior essence function. It is still the case that the boundary behavior of a well-defined domain assembly can be unpredictable. It is difficult to control this boundary behavior.
A protein is a triplet P=(A, S_0, F) where A is an abstract domain assembly, S_0 is a state for the domain assembly called the initial state and F is a true behavior function for A which is such that its associated realization function always has an initial state equal to S_0. Any abstract domain assembly can be made into a protein in potentially different ways.
FIXME: Also need to specify initial state for the state machine of each domain. Carry through rest.
A protein can be seen as a network of pipes and machines which carry and transform various types of liquid.
Proteins may have many properties, derived from properties of domain assemblies. There are finite proteins, spacing independent proteins, well-defined proteins. We don't recall all the details here. The reader is invited to read Combinations. This appendix contains an exploration of various proteins and describes their properties. Some of the properties discussed have not been introduced yet.
Later on we will see that the Monod Culture evolutionary framework can not avoid non-finite proteins, non-well-defined proteins, etc. Nevertheless, these properties are very much desirable. Indeed, any task that any protein can do can be done by one or a set of well-defined proteins, and probably better. (FIXME: Prove this!)
FIXME: Deleterious behavior. Non-productive behavior. Good behavior.
FIXME: Proteins inside an Incubator. Protein programs containing more than one protein.